Определить радиусы двух внешне касающихся кругов, если расстояние между их центрами равно d, а угол между общими внешними касательными равен φ.

По условию ∠BAE = φ (рис.).

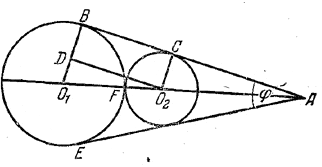
Следовательно, ∠BAO₁ = ^φ/₂ . Требуется определить R = O₁B и r = О₂С.

Имеем

R+ r = О₁F+FO₂ = O₁O₂ = d

и

R- r = О₁B - O₂C = О₁D

Из прямоугольного треугольника O₁DO₂, где ∠O₁O₂D = ∠BAO₁ = ^φ/₂ находим

O₁D = O₁O₂ • sin ^φ/₂ , т. е. R- r = d sin ^φ/₂.

Из двух полученных уравнений находим

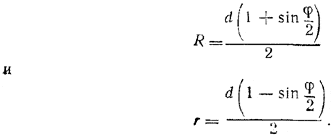
Заменяя sin ^φ/₂ через cos (90° - sin ^φ/₂), можно преобразовать эти выражения.

Ответ: R = d cos²(45°- ^φ/₄) , r = d sin²(45°- ^φ/₄)