Найти двугранный угол между боковыми гранями правильной треугольной пирамиды, если двугранный угол, образуемый боковой гранью с основанием, равен α.

Пусть ВМ и СМ - перпендикуляры, опущенные из вершин основания В и С на боковое ребро SA.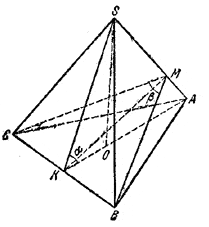


Образованный ими ∠ВМС является искомым. Обозначим его через β. Очевидно,

sin β/2= BK/ВM (1)

Пусть а - сторона основания пирамиды. Тогда

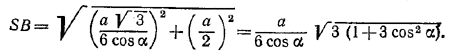
Из равнобедренного треугольника ASB легко находим его высоту ВМ:





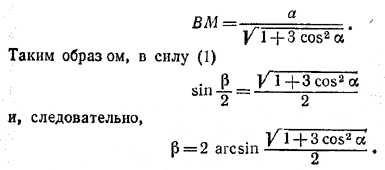
Похожие примеры:
Основанием пирамиды служит квадрат. Две противоположные грани — равнобедренные треугольники, одна из них образует с основанием внутренний угол β, а другая — внешний острый угол α. Высота пирамиды равна Н. Найти объем пирамиды и углы, образованные двумя другими боковыми гранями с плоскостью основания. Смотреть решение→
Двугранный угол при боковом ребре правильной шестиугольной пирамиды равен φ. Определить плоский угол при вершине пирамиды. Смотреть решение→
В основании прямой призмы лежит прямоугольный треугольник с катетом а и противолежащим ему углом α. Через вершину прямого угла нижнего основания проведена плоскость, параллельная гипотенузе, под углом β= 90°— α к противолежащей боковой грани и пересекающая ее. Определить объем части призмы между ее основанием и сечением и боковую поверхность призмы, если известно, что боковая грань, проходящая через катет а, равновелика сечению призмы. Определить, при каком значении угла αплоскость сечения пересекает боковую грань, проходящую через гипотенузу основания. Смотреть решение→