На стороне АВ прямоугольника ABCD найти такую точку Е, из которой стороны AD и DC были бы видны под равными углами.
При каком соотношении между сторонами прямоугольника задача разрешима?

Если ∠AED = ∠DEC (рис.), то также ∠CDE = ∠DEC, откуда CE = CD.

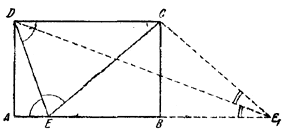
Следовательно, Е есть точка пересечения стороны АВ с окружностью, описанной из центра С радиусом CD. Задача разрешима, если АВ > ВС, причем имеет два решения, когда АВ > ВС, и одно решение, когда АВ =ВС. (Точка E₁на рисунке соответствует второму решению).