Определить углы прямоугольного треугольника, зная, что радиус описанного около него круга относится к радиусу вписанного круга как 5:2.

Пусть R — радиус описанного круга и r —радиус вписанного.

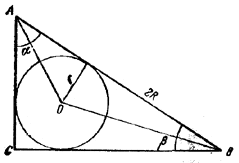
Тогда AB = 2R, а также

AB = r ctg ^α/₂ + r ctg ^β/₂.

Отсюда

ctg ^α/₂ + ctg ^β/₂ =^2R/_r = 5

Кроме того, ^α/₂ + ^β/₂= ^π/₄и ctg (^α/₂ + ^β/₂) = 1, т.е.

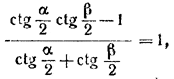
откуда

ctg ^α/₂ ctg ^β/₂ = 6.

Следовательно, ctg ^α/₂и ctg ^β/₂ равны корням квадратного уравнения

х²— 5х + 6 = 0.

Окончательно получаем:

α = 2arctg ¹/_{2 ,} β = 2arctg ¹/₃