Решить уравнение sin х + cos x = 1

Возведя обе части данного уравнения в квадрат, мы получим:

sin² х + 2 sin x cos x + cos² x = 1,

но sin² х + cos² x = 1. Поэтому 2 sin x cos x = 0. Если sin x = 0, то х = nπ; если же
cos x, то х = ^π/₂ + kπ. Эти две группы решений можно записать одной формулой:

х = ^π/₂ n

Поскольку обе части данного уравнения мы возводили в квадрат,то не исключена возможность, что среди полученных нами корней имеются посторонние. Вот почему в этом примере, в отличие от всех предыдущих, необходимо сделать проверку. Все значения х = ^π/₂ n можно разбить на 4 группы

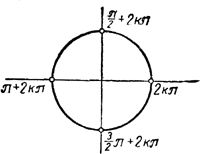
1. х = 2kπ    (n = 4k)
2. х = ^π/₂ + 2kπ   (n = 4k + 1)
3. х = π + 2kπ   (n = 4k + 2)
4. х = ^3π/₂ + 2kπ   (n = 4k + 3)

При х = 2kπ sin x + cos x = 0 + 1 = 1. Следовательно, х = 2kπ - корни данного уравнения.

При х = ^π/₂ + 2kπ. sin x + cos x = 1 + 0 = 1 Значит, х = ^π/₂ + 2kπ - также корни данного уравнения.

При х = π + 2kπ sin x + cos x = 0 - 1 = - 1. Поэтому значения х = π + 2kπ не являются корнями данного уравнения. Аналогично показывается, что х = ^3π/₂ + 2kπ. не являются корнями.

Таким образом, данное уравнение имеет следующие корни: х = 2kπ и х = ^π/₂ + 2mπ., где k и m - любые целые числа.