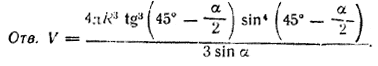В конус с радиусом основания R и углом α между высотой и образующей вписан шар, касающийся основания и боковой поверхности конуса. Определите объем части конуса, расположенной над шаром.

На рис. изображено осевое сечение конуса и вписанного в него шара. Искомый объем V получается вычитанием объема шарового сегмента MEN из объема конуса MCN.

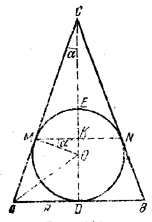
Следовательно,

V = ^π/₃ • МК² • КС - π • КЕ² ( r -¹/₃ КE),

где r есть радиус шара. Из треугольника AOD находим

r = OD = AD • tg ^∠DAC/₂ = R tg (45° - ^α/₂).

Теперь из треугольника ОМК, где ∠ ОМК = α (стороны углов ОМК и МСК взаимно перпендикулярны), имеем

MK = OM • cos α = r cos α и OK = r sin α.

Значит, КЕ = ОЕ- OK = r (1 - sin α). Наконец, КС = МК. • ctg α = r cos α ctg α. Следовательно,

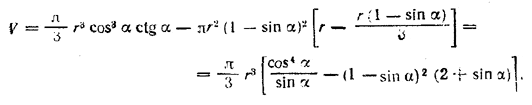
Это выражение можно упростить. Вынесем за скобки (1 - sin α )², предварительно преобразовав cos⁴ α; именно,

cos⁴ α =( l - sin² α )²=( l - sin α )² (1+ sin α )².

Теперь имеем

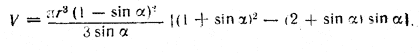
Выражение в квадратных скобках равно единице. Получаем

Сюда подставляем найденное выражение

r = R tg (45° - ^α/₂).

Кроме того, можно использовать формулу

1 - sin α = 2 sin² (45° - ^α/₂).