В правильной четырехугольной призме через середины двух смежных сторон основания проведена плоскость, пересекающая три боковых ребра и наклоненная к плоскости основания под углом α. Определить площадь полученного сечения и острый угол его, если сторона основания призмы равна b.
Соединяем середины К и L (рис.) сторон АВ и AО.
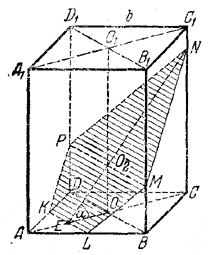
Через точку Е, где KL пересекает AС, проводим прямую EN (угол NEC изображает линейный угол двугранного угла α). Через точку О2, где EN пересекается с OO1 (изображение оси), проводим PM||BD. Пятиугольник KLMNP изображает сечение. Доказательство вытекает из нижеприводимого решения.
Решение. Так как KL||BD, то плоскость KLMNP (проходящая через KL) пересекается с диагональнoй плоскостью DBB1D1 (проходящей через BD) по прямой РМ, параллельной KL и BD. Ось призмы ОО1 лежит в диагональной плоскости DBB1D1 и, следовательно, пересекается с прямой РМ. С диагональной плоскостью АСС1А1 плоскость KLMNP пересекается по прямой NE (Е - середина KL); эта прямая тоже пересекает ось OO1. Но так как плоcкость KLMNP, в которой лежат прямые РМ и EN, пересекается с осью ОО1 только в одной точке О2, то обе прямые EN и МР проходят через эту точку, т. е. точка пересечения прямых РМ и EN лежит на оси ОO1 . Прямые ЕС и EN перпендикулярны к KL (теорема о трех перпендикулярах); значит, ∠ CEN = α.
Площадь S пятиугольника KLBCD равна площади квадрата ABCD без площади треугольника AKL, так что ![]()
Площадь Scеч. пятиугольника KLMNP определяется по теореме, доказанной в предварительном замечании к задаче 196 . Имеем 7/8b2 = Scеч. cos α, т. е.
![]()
Сравнивая треугольники MO2N и ВОС (у них BO = MO2 и MN > BC), убеждаемся, что ∠ MNO2 < ∠ BCO; a так как ∠ ВСО = 45°, то ∠ MNO2 < 45° и, следовательно, угол φ =∠ MNP - острый.
Остальные углы сечения-тупые (острый угол NMO2= 90°- ∠ MNO2 больше 45°; угол MLK равен 180°- ∠ LMO2 = 180°- ∠ NMO2). Из треугольника MO2N имеем