Прямой параллелепипед, имеющий в основании ромб, со стороной а и острым углом α, пересечен плоскостью, проходящей через вершину угла α и дающей в сечении ромб с острым углом ^α/₂, Определить площадь этого сечения.

Ср. предыдущую задачу. Площадь S_cеч. ромба BNKM (рис.) равна

S_cеч. = ¹/₂ MN • ВК = 2МО₁ • ВО₁.

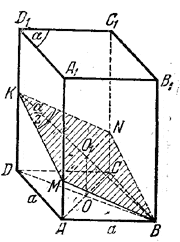
Из треугольника MO₁B, где ∠ MBO₁= ^α/₄ , находим

ВО₁ = МО₁ • ctg ^α/₄ .

Следовательно,

S_cеч. = 2 • MO₁² • ctg ^α/₄ = 2• AO² • ctg ^α/₄

Отрезок АО находим из треугольника AОВ, где АВ = а и ∠ AВО= ^α/₂.

Получаем

AО = a sin ^α/₂

Ответ: S_cеч.= 2а² sin^{2 α}/₂ ctg ^α/₄.