В основании пирамиды ромб со стороной а. Две соседние грани составляют с плоскостью основания угол α, третья боковая грань составляет с плоскостью основания угол β(доказать, что и четвертая боковая грань наклонена к основанию под тем же углом). Высота пирамиды Н. Найти объем пирамиды и полную поверхность ее.

Пусть ABE (рис., a) -первая, а ADE - вторая боковая грань.

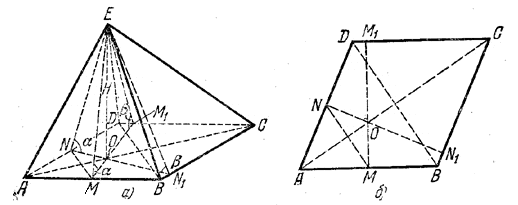
По условию они наклонены к основанию под одним и тем же углом α. Отсюда следует, что точка О, через которую проходит высота, лежит на диагонали АСК Действительно, если из точки О (рис., б) опустить перпендикуляры ОМ и ОN *) на стороны АВ и AD, то ∠ OME = α и ∠ ONE = α (доказать!);

*) На пространственном чертеже (рис., а) один из этих перпендикуляров, например ОМ, можно изобразить произвольной прямой, но после этого второй строится вполне определенным образом, так как прямая MN должна быть параллельна диагонали BD, Это легко доказать на плоском чертеже (рис., б),

следовательно,

ОМ = H ctg α и ON = H ctg α.

т. е. OM = ON. Значит, точка О лежит на биссектрисе угла BAD, т. е. на диагонали АС ромба ABCD.

Но тогда также имеем OM₁ = ON₁ (OM₁ и ON₁ - продолжения ОМ и ON), откуда следует равенство треугольников ОМ₁Е и ON₁E и, значит, ∠ON₁E = ∠ОМ₁Е, что и требовалось доказать.

Из треугольника ОМЕ находим ОМ = Н ctg α, a из треугольника ОМ₁Е имеем
ОМ₁= Н ctg β. Следовательно, высота h ромба равна h = MM₁ = H (ctg α + ctg β).

Значит,

V = ¹/₃S_ocн. H = ¹/₃ ahH = ¹/₃ aH² (ctg α + ctg β),

S_п.= S_ocн. + 2S_ABE + 2S_BEC = a ( h + ME + N₁E)

где МE = ^H/_{sin α} N₁E = ^H/_{sin β}

Тогда

Выразив числители и знаменатели через ^α/₂ и ^β/₂ и сократив дроби, получим