Доказать, что любой плоский угол произвольного четырехгранного угла меньше суммы трех других плоских углов.

Пусть А, В, С и D - произвольные точки, лежащие на ребрах четырехгранного угла с вершиной E (рис.).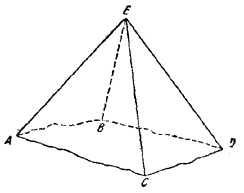

Докажем, например, что

∠CED < ∠СЕА+∠АЕВ+ ∠BED. (1)

Проведем плоскость СЕВ. По свойству плоских углов трехгранного угла

∠CED < ∠CEB + ∠BED (2)

и по той же причине

∠СЕВ < ∠СЕА + ∠АЕВ. (3)

Из неравенств (2) и (3) следует (1). Неравенство (1), таким образом, доказано.

Легко понять, что наше рассуждение сохраняет силу и в том случае, когда четырехгранный угол не является выпуклым, т. е. когда ребро ED оказывается по другую сторону плоскости СЕВ.