Даны окружность К радиуса r и ее хорда АВ длиной 2a. Пусть CD - подвижная хорда той же окружности, имеющая постоянную длину 2b. Найти геометрическое место точек пересечения прямых АС и BD

Искомое геометрическое место есть окружность, проходящая через концы хорды АВ и одну из точек M₁, получаемых указанным в условии построением.

Доказательство. Предварительно введем некоторые обозначения. Найдется одно и только одно такое положение C₁D₁ хорды CD, когда C₁D₁ || AB и когда на данной окружности К можно выбрать такое направление обхода v, при движении в котором концы хорд будут встречаться в последовательности А, В, C₁ , D₁ (этот выбор может не быть определенным только в случае равенства AB = CD, когда прямые АС и BD параллельны). Обозначим через α ту из дуг АВ данной окружности К, на которой лежат точки С₁, D₁, через β -другую дугу АВ и через γ -ту из дуг C₁D₁, на которой нет точек А, В. Далее, обозначим через М₁ точку пересечения прямых АС₁ и BD₁. Точка M₁ лежит внутри К. Пусть К₁-окружность, описанная около \(\Delta\)АВМ₁ (рис. 133). Докажем, что при любом сдвинутом положении хорды CD точка пересечения прямых АС и BD будет находиться на К₁

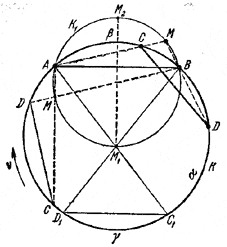
Пока обе точки С, D лежат на дуге α , точка М будет находиться внутри К, а тогда

∠AMB = ¹/₂(β + γ). (1)

Если же хотя бы одна из точек С, D попадет на дугу β, то точка М будет лежать вне К и тогда

∠AMB = ¹/₂(α - γ). (2)

В первом случае М лежит на дуге АМ₁В окружности К₁, так как согласно (1) ∠АМВ не зависит от положения CD и, значит, равен ∠АМ₁В. Во втором случае, ввиду того что сумма правых частей (1) и (2) равна

¹/₂(α + β) = ¹/₂ • 2π = π,

точка М лежит на внешней относительно К дуге АВ окружности K₁.

Очевидно, верно и обратное, т. е. любая точка М окружности K₁ может быть получена при надлежащем выборе положения хорды CD.