Прямая, параллельная основанию треугольника, площадь которого равна S, отсекает от него треугольник с площадью, равной q. Определить площадь четырехугольника, три вершины которого совпадают с вершинами меньшего треугольника, а четвертая лежит на основании большего треугольника.

По условию площадь треугольника ABC равна S, а площадь треугольника KBM равна q.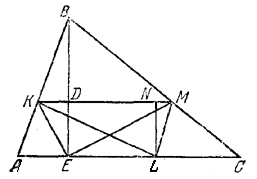

Три вершины четырехугольника совпадают с точками K, В и М; четвертую же вершину L можно взять на стороне АС произвольно. Действительно, площадь S₁ четырехугольника LKBM есть сумма площади q треугольника КВМ и площади треугольника KLM, а последняя не меняется при движении вершины L по прямой АС, параллельной основанию КМ. Пусть высота BE треугольника ABC проходит через точку Е основания АС. Поместив точку L в точку Е, получим четырехугольник КВМЕ, диагонали которого взаимно перпендикулярны; следовательно, S₁ = ¹/₂KM • BE.
А так как q = ¹/₂KM • BD, то S₁ : q = ВE : BD.

Но из подобия треугольников АВC и KBM имеем S : q = BE² : BD².
Следовательно,

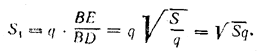
Замечание. Если точка L не совпадает с точкой Е, то решение видоизменяется так: находим

S₁=¹/₂ KM • BD + ¹/₂KM • NL = ¹/₂KM (BD + ML) = ¹/₂КМ • BE,

и дальше аналогично.

Отв. √Sq