Треугольник ABC разбит на три равновеликие фигуры прямыми, параллельными стороне АС. Вычислить, на какие части разбили эти прямые сторону АВ, равную а.

Так как S_EBF = S_DEFG = S_ADOC, тo площадь треугольника EBF вдвое меньше площади треугольника DBG и втрое меньше площади треугольника ABC.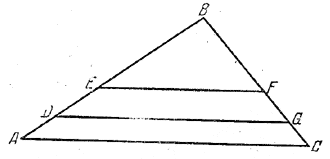

Так как эти треугольники подобны, то ЕВ² : DB² : AB² = 1 : 2 : 3. По условию АВ =а следовательно, ЕВ = ^a/_√3 и DB = ^a√2/_√3.

Отв. Сторона АВ разбита на части ^a/_√3 , ^a/_√3 (√2 - 1 ) и ^a/_√3( √3 - √2)