В конус вписан шар радиуса r. Найти объем конуса, зная, что плоскость, касающаяся шара и перпендикулярная к одной из образующих конуса, отстоит от вершины конуса на расстоянии d.
Возможны два случая: 1) вершина конуса и шар лежат по разные стороны от касательной плоскости; 2) вершина конуса и шар лежат по одну сторону от касательной плоскости.Рассмотрим первый случай. Проведем плоскость через ось конуса и образующую конуса ВС, о которой говорится в условии задачи.
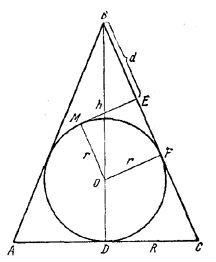
Эта плоскость в сечении с конусом даст треугольник ABC, в сечении с шаром-окружность С центром О; плоскость, перпендикулярная к ВС, будет пересечена по прямой ME (М.-точка касания).
Проведем BD ⊥ AC и OF ⊥ ВС Пусть BD = h, OD = OF = r, CD = R. Очевидно, OMEF - квадрат, поэтому
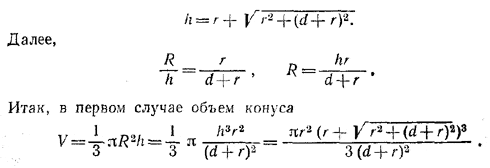
Во втором случае задача решается аналогично. Объем конуса оказывается равным
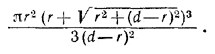
Похожие примеры: