В шар радиуса R вписан конус, боковая поверхность которого в k раз больше площади основания. Найти объем конуса.
Пусть h -высота конуса, r -радиус основания, l - образующая конуса и α - угол между образующей и высотой.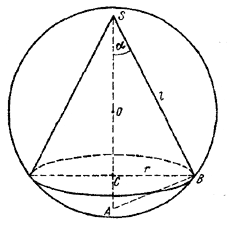
По условию задачи имеем πrl = kπr2; отсюда l = kr и, следовательно, sin α= 1/k . Из прямоугольного треугольника ABS получаем:
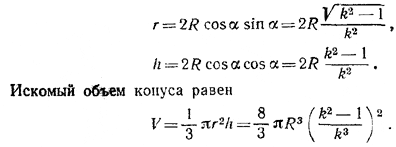
Похожие примеры: