Правильная четырехугольная пирамида со стороной основания, равной а, и двугранным углом при основании, равным 2α, пересечена плоскостью, делящей пополам двугранный угол при основании. Найти площадь сечения.

Пусть ABC'D'- указанное сечение пирамиды OABCD. Через вершину О пирамиды и середину ее ребер АВ и CD проведем вспомогательную плоскость OPN.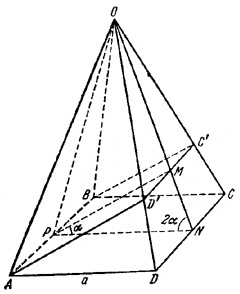

Легко видеть, что плоскость OPN перпендикулярна к АВ и CD, а отрезки ОР и ON равны.

Применяя теорему синусов к треугольнику ОРМ, находим:

Так как D'C' || DC, то

Применяя теорему синусов к треугольнику PMN, находим

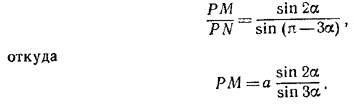
Теперь получаем искомую площадь сечения ABC'D':