Даны два равных полукруга, касающихся друг друга так, что диаметры их лежат на одной прямой. Проводим к ним общую касательную и вписываем первый круг, касающийся этой прямой и двух данных кругов; затем вписываем второй круг, касающийся первого и двух данных, затем третий круг, касающийся второго и двух данных, и т. д. до бесконечности. Пользуясь этим построением, доказать, что сумма дробей
\(\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + \frac{1}{4 \cdot 5} +...+ \frac{1}{n(n + 1)}\)
при безграничном возрастании n стремится к 1, т. е.\(\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} +...+ \frac{1}{n(n + 1)} = 1\)
Пусть R — радиус данных полуокружностей. Если r1, r2, ...., rn — радиусы вписываемых кругов, d1, d2, ..., dn — их диаметры,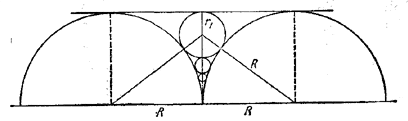
то ясно, что при безграничном возрастании n сумма d1 + d2 +...+ dn стремится к R, т. е.
d1 + d2 +...+ dn +... = R. (1)
Кроме того, имеем:
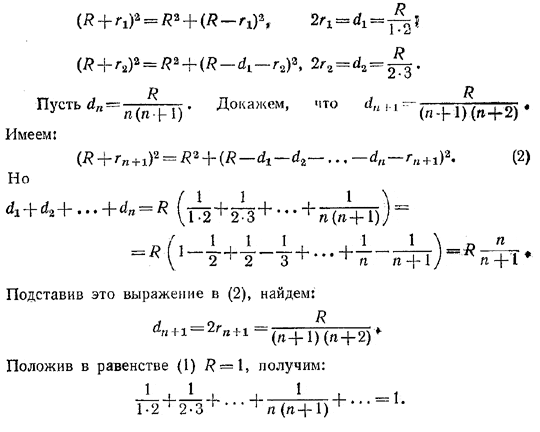
Похожие примеры: