Доказать, что прямые, соединяющие последовательно центры квадратов, построенных на сторонах параллелограмма и примыкающих к нему извне, образуют также квадрат.

Пусть О₁, О₂, О₃, О₄ — центры квадратов, построенных на сторонах параллелограмма ABCD.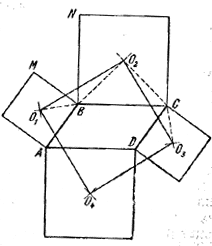

Имеем:

\(\Delta\)О₁ВО₂ = \(\Delta\)О₃СО₂,

так как О₁В= О₃С, ВО₂ = СО₂ и ∠О₁ВО₂ = ∠MBN + ^π/₂= ∠DCB + ^π/₂ = ∠О₃СО₂

Следовательно,

О₁О₂ = О₃О₂ и ∠О₁О₂О₃ = ∠О₁О₂В + ∠BO₂C — ∠О₃О₂C = ∠BO₂C = ^π/₂

Аналогично доказывается, что О₂О₃ = О₃О₄ = О₄О₁ и

∠О₂О₃О₄ = ∠ О₃О₄О₁ = ∠О₄О₁О₂ = ^π/₂.

Следовательно, О₁О₂О₃О₄ — квадрат.

---

Вариант 2

Построим (рис.) треугольники OEO₁и OFO₂ (точки В и F - середины сторон параллелограмма).

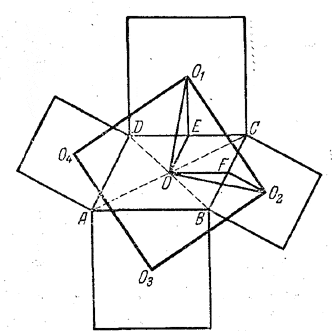
Эти треугольники равны. Действительно, OE = FC, а из условия следует, что FC = O₂F. Следовательно, OE=O₂F. Так же докажем, что O₁E= OF.

Углы OEO₁и OFO₂ (оба они тупые) равны, так как их стороны взаимно перпендикулярны. Из равенства треугольников OEO₁и OFO₂ следует, что ОО₁ = ОО₂ и что ∠OO₁E = ∠O₂OF. А так как О₁Е и OF образуют прямой угол, то и прямые ОО₁ и ОО₂ образуют прямой угол. Значит, треугольник О₁О₂О - равнобедренный и прямоугольный. Таковы же и треугольники O₂O₃O, O₃O₄O и O₄O₁O. Отсюда следует, что O₁O₂O₃O₄ есть квадрат.