Доказать, что если диагонали двух четырехугольников соответственно равны и пересекаются под равными углами, то четырехугольники равновелики.

Найдем выражение для площади четырехугольника через диагонали и угол между диагоналями. Пусть О — точка пересечения диагоналей четырехугольника ABCD и ∠ВОА = α.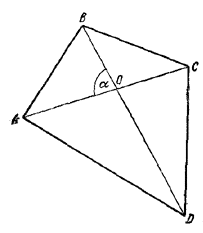

Тогда площадь данного четырехугольника равна

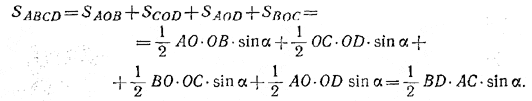
Из этой формулы и следует справедливость доказываемого утверждения.