Доказать, что медиана треугольника меньше полусуммы сторон, ее заключающих, и больше разности между этой полусуммой и половиной третьей стороны.

Пусть ВО - медиана в треугольнике ABC; достроим треугольник ABC до параллелограмма ABCD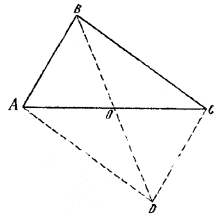


Из треугольника BCD имеем 2 ВО < BC + CD, и так как CD = AB, то

Из \(\Delta\)AOB и \(\Delta\)BOC имеем:

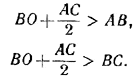
Сложив эти неравенства, получим:





Похожие примеры:
Данный треугольник ABC пересечь прямой DE, параллельной ВС, так, чтобы площадь треугольника BDE равнялась заданной величине k2. При каком соотношении между k2и площадью треугольника ABC задача разрешима и сколько она имеет решений?  Смотреть решение→
Найти отношение площади треугольника ABC к площади другого треугольника, стороны которого равны медианам треугольника ABC.  Смотреть решение→
В треугольнике ABC через точку пересечения биссектрис углов В и С проведена параллельно ВС прямая MN до пересечения в точках М и N соответственно со сторонами АВ и АС. Найти зависимость между отрезками MN, ВМ, CN.
Разобрать случаи:
  1. обе биссектрисы внутренние;
  2. обе биссектрисы внешние;
  3. одна из биссектрис внутренняя, другая внешняя.
Когда М и N совпадут?  Смотреть решение→