Углы при 2-х параллельных прямых и секущей
Мы знаем, что две прямые параллельны, если при пересечении их третьей прямой равны соответственные углы, или внутренние, или внешние накрест лежащие углы, или сумма внутренних, или сумма внешних односторонних углов равна 2d. Докажем, что верны и обратные теоремы, а именно:
Если две параллельные прямые пересечены третьей, то:
1. соответственные углы равны;
2. внутренние накрест лежащие углы равны;
3. внешние накрест лежащие углы равны;
4. сумма внутренних односторонних углов равна 2d;
5. сумма внешних односторонних углов равна 2d.
Докажем, например, что если две параллельные прямые пересечены третьей прямой, то соответственные углы равны.
Пусть прямые АВ и СD параллельны, а МN - их секущая (рис.). Докажем, что соответственные углы 1 и 2 равны между собой.
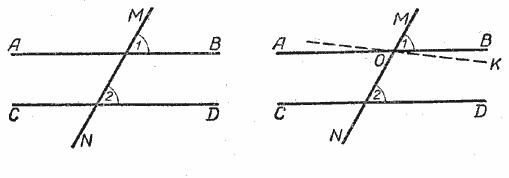
Допустим, что ∠1 и ∠2 не равны. Тогда при точке О можно построить ∠МОК, соответственный и равный ∠2 (рис.).
Но если ∠МОК = ∠2, то прямая ОК будет параллельна СD.
Получили, что через точку О проведены две прямые АВ и ОК, параллельные прямой СD. Но этого быть не может.
Мы пришли к противоречию, потому что допустили, что ∠1 и ∠2 не равны. Следовательно, наше допущение является неправильным и ∠1 должен быть равен ∠2, т. е. соответственные углы равны.
Установим соотношения между остальными углами. Пусть прямые АВ и СD параллельны, а МN - их секущая (рис.).
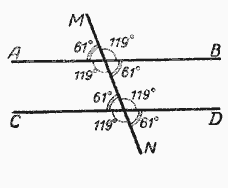
Мы только что доказали, что в этом случае соответственные углы равны. Положим, что какие-нибудь два из них имеют по 119°. Вычислим величину каждого из остальных шести углов. На основании свойств смежных и вертикальных углов мы получим, что четыре угла из восьми будут иметь по 119°, а остальные - по 61°.
Оказалось, что как внутренние, так и внешние накрест лежащие углы попарно равны, а сумма внутренних или внешних односторонних углов равна 180° (или 2d).
То же самое будет иметь место и при любом другом значении равных соответственных углов.
Следствие 1. Если каждая из двух прямых АВ и СD параллельна одной и той же третьей прямой МN, то первые две прямые параллельны между собой.
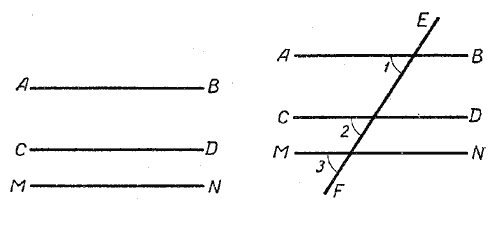
В самом деле, проведя секущую ЕF (рис.), получим:
а) ∠1 = ∠3, так как АВ || МN; б) ∠ 2 = ∠3, так как СО || МN.
Значит, ∠1 = ∠2, а это углы соответственные при прямых АВ и СD и секущей ЕF, следовательно, прямые АВ и СD параллельны.
Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
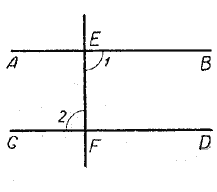
В самом деле, если ЕF ⊥ АВ, то ∠1 = d; если АВ || СD, то ∠1 = ∠2.
Следовательно, ∠ 2 = d т. е. ЕF ⊥ СD .