Центральный угол

Центральным углом называется угол, образованный двумя радиусами одного и того же круга.

∠АОВ — центральный (рис. 90). Дуга АВ называется соответствующей центральному углу АОВ.

Полному углу соответствует вся окружность.

Развёрнутому углу соответствует дуга, равная половине окружности.

Прямому углу соответствует дуга, равная ¹/₄ части окружности.

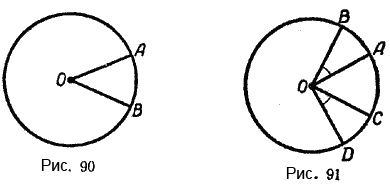
Теорема. Если в одном и том же круге два центральных угла равны, то равны, соответствующие им дуги.

Докажем это. Возьмём окружность, построим в ней два равных центральных угла (рис. 91). Пусть ∠АОВ = ∠СОD. Вращая ∠AОВ вокруг центра О, можно совместить его с углом СОD, так как эти углы равны между собой (такое условие принято нами). Если же углы АОВ и СОD совместятся, то в силу равенства радиусов совместятся и концы дуг АВ и СD. (Точка А совместится с точкой D, и точка В совместится с точкой С.) Следовательно, совместятся и сами дуги АВ и СD, так как все точки этих дуг находятся на одинаковом расстоянии от центра, т. е. \(\breve{AB}\) = \(\breve{CD}\).

Докажем обратную теорему.

Теорема. Если в одном и том же круге две дуги равны, то равны и соответствующие им центральные углы.

В самом деле, так как дуга АВ равна дуге СD (рис. 91), то дуга АВ, скользя по окружности, может совместиться с дугой СD, при этом точки А и В совместятся соответственно с точками D и С. Но в этом случае радиус ОА совместится с радиусом ОD, а радиус ОВ совместится с радиусом ОС, т. е. угол АОВ равен углу СОD.

Эти две теоремы справедливы и для равных кругов.

Вторая теорема называется обратной по отношению к первой потому, что в первой теореме доказывается равенство дуг, если равны центральные углы, во второй же теореме, наоборот, доказывается равенство центральных углов, если равны дуги.