Биссектриса угла
Все точки биссектрисы угла обладают одним общим свойством: каждая из них находится на одинаковом расстоянии от сторон этого угла.
Пусть луч АО является биссектрисой угла ВАС. Возьмем какую-нибудь произвольную точку Е на биссектрисе АО и опустим из нее на стороны угла перпендикуляры: ЕN ⊥ АС и ЕМ ⊥ AB. Мы получим два треугольника АЕМ и АЕN.
Треугольники эти прямоугольные по построению, сторона АЕ является общей, а ∠1 = ∠2 по условию.
Отсюда следует, что ΔАМЕ = ΔАNЕ и ЕМ = ЕN, т. е. точка Е одинаково удалена от сторон угла ВАС. Так как точка Е была взята на биссектрисе произвольно, то можно утверждать, что и всякая точка биссектрисы АО одинаково удалена от сторон ∠ВАС.
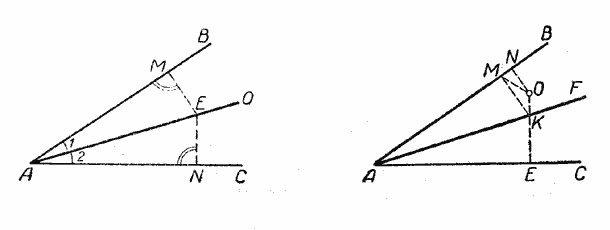
Всякая же точка О, находящаяся не на биссектрисе АF (рис.), неодинаково удалена от сторон этого угла.
Опустим из точки О перпендикуляры ОN и ОЕ на АВ и АС и докажем, что ОN не равняется ОЕ.
Из точки К пересечения биссектрисы АF и перпендикуляра ОЕ опустим перпендикуляр КМ на АВ. По доказанному ранее КМ = КЕ, кроме того, МК + КO > МО, тогда и
ЕК + КО > МО, т. е. ОЕ > ОМ. Но МО > NO, так как МО — гипотенуза, а NO — катет в треугольнике МОN. Поэтому ОЕ и подавно больше ОN.
Следовательно, всякая точка, не лежащая на биссектрисе угла, неодинаково удалена от сторон этого угла.
Биссектриса угла есть геометрическое место точек, каждая из которых одинаково удалена от сторон этого угла.
Она является осью симметрии угла.
Задача. Построить биссектрису угла, т. е. разделить угол пополам.
Дан угол АBС, требуется разделить его пополам.
На сторонах данного угла АBС (рис.) от его вершины B отложим равные отрезки ВМ и BN.
Из точек М и N одним и тем же радиусом описываем дуги.
Точку К пересечения этих дуг соединим с точкой B. Луч ВК будет биссектрисой данного угла АBС.
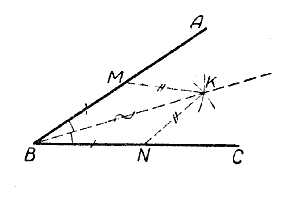
Чтобы доказать это, соединим точку К с точками М и N и сравним треугольники ВМК и BNК:
BM=BN; MK=NK - по постpoению
ВК - общая сторона.
Следовательно, Δ ВМК = Δ ВNK
Отсюда ∠МВК =∠NВК, так как они лежат против равных сторон в двух равных треугольниках, т. е. ВК служит биссектрисой угла АBС.