Рассмотрим правильную пирамиду ABCDS, в которой проведено сечение KLMNP, представляющее собой правильный пятиугольник со стороной a (рис.).

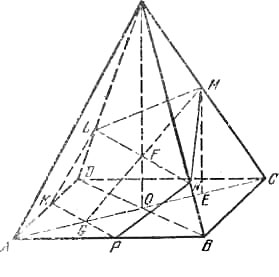
Пусть диагональ основания пирамиды равна b, боковое ребро l. Обозначим также |SM| = xl, |SN| = yl. Поскольку пятиугольник KLMNP - правильный,

$$ |LN|=2a cos\frac{\pi}{5}=\frac{1+\sqrt5}{2}a = \mu a,\\ \frac{|MF|}{|FG|}=\frac{1-cos\frac{2\pi}{5}}{cos\frac{\pi}{5}+cos\frac{2\pi}{5}} $$

Имеем: |KP| = a, |GO| = (b - a)/2. С другой стороны,

$$ |OE| = |OC|\frac{|SM|}{|SC|}=\frac{b}{2}x, \\ |ME|=|SO|\frac{|MC|}{|SC|}=h(1-x),\\ |FO|=h(1-y) $$

где h - высота пирамиды, следовательно,

$$ \frac{|GO|}{|FO|}=\frac{|OE|}{|ME|-|FO|},\;\;|GO|=\frac{(1-y)xb}{2(y-x)} $$

Приравнивая найденные выражения для |GO|, получим уравнение

$$ \frac{(1-y)xb}{y-x}=b-a\;\;\; (1)$$

Далее:

$$ \frac{|OE|}{|GO|}=\frac{|MF|}{|FG|}=\lambda $$

откуда

$$ \frac{y-x}{1-y}=\lambda\;\;\;(2) $$

Поскольку |LN| = μ a, |LN| = у|DB|, то

$$ yb = \mu a\;\;\;(3) $$

И, наконец, рассмотрим ΔPNB, в котором |PN| = а, |NB| = (1 - y)l, \(|PB| = \frac{b-a}{2}\sqrt2, cos \angle{PBN} = cos \angle{ABS} = \frac{b}{2\sqrt2 l}\).

По теореме косинусов получим

$$ a^2=(1-y)^2l^2 + \frac{(b-a)^2}{2} - \frac{(1-y)(b-a)b}{2}\;\;\;(4) $$

Учитывая, что

$$ \mu=\frac{\sqrt5+1}{2},\;\;\lambda=\frac{\sqrt5-1}{2} $$

из уравнений (1)-(3) найдем

$$ y=\frac{\sqrt5-1}{2},\;\;b=\frac{\sqrt5+3}{2}a $$

после чего из уравнения (4) получим

$$ l^2=\frac{a^2(7+3\sqrt5)}{4}=\frac{b^2}{2} $$

Таким образом, объем пирамиды равен

$$ \frac{1}{3}\cdot\frac{b^2}{2}\sqrt{l^2-\frac{b^2}{4}}=\frac{b^3}{12}=\frac{(9+4\sqrt5)}{12}a^3 $$