$$ V = S \cdot H $$

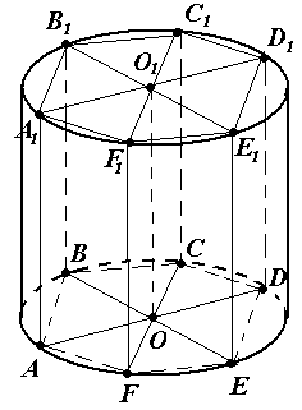
1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра.

2) по условию V = 10π, т.е. \(\pi R^2H = 10\pi \Rightarrow R^2 H =10 \).

3) так как сторона правильного шестиугольника равна радиусу описанной около него окружности, то R = а.

4) выразим радиус основания вписанного цилиндра r через радиус описанного цилиндра R: \( r=\frac{\sqrt3}{2}R\).

5) запишем формулу вычисления объёма вписанного в призму цилиндра: V = S • H, т.е.:

$$ V=\pi r^2 H = \pi(\frac{\sqrt3}{2}R)^2\cdot H = \pi\frac{3}{4}(R^2 H) = \frac{3}{4}\pi \cdot 10 = 7,5\pi $$

Ответ: 7,5π.