$$ V = S \cdot H $$

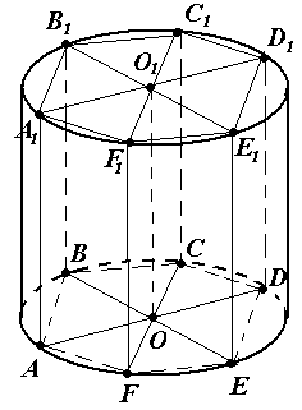
1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, т.е. Н = 4.

2) по условию V = 16π, т.е. $$ \pi R^2H = 16\pi \Rightarrow R^2 = \frac{16\pi}{\pi H}, R=2 $$

3) так как сторона правильного шестиугольника равна радиусу описанной около него окружности, то а = 2.

4) Найдем площадь основания призмы по формуле: \(S=\frac{a^2 \cdot 3\sqrt3}{2} = 6\sqrt3\).

5) вычислим объём призмы: V = 6√3 * 4 = 24√3.

Ответ: 24√3.