В треугольнике ABC AC=BC=15, AB=18. Найдите синус внешнего угла при вершине A.

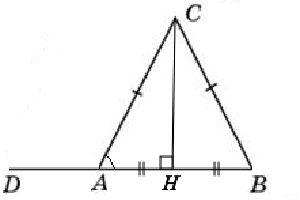
Найдем сначала sinA.

Треугольник ACB – равнобедренный. Построим высоту CH, она же будет являться и медианой.

AH = HB = AB/2 = 18/2 = 9

Из треугольника AHC по теореме Пифагора найдем CH:

CH2 = AC2 – AH2 = 152 – 92 = 225 – 81 = 144

CH = 12

Теперь выразим синус внешнего угла CAD через синус внутреннего угла CAH.

CAD = 180° – CAH (смежные углы)

Заметим, что sin(180° – x) = sinx по формулам приведения.

(180° – x попадает во вторую четверть, где синус положителен. См. рисунок)

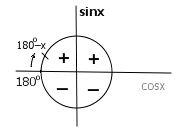
sinCAD = sin(180° – CAH) = sinCAH = 0,8