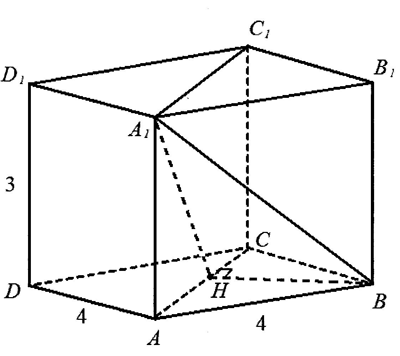
Из точки В проведем перпендикуляр ВН к АС. А₁Н – проекция А₁В на плоскость АА₁С. Значит, угол ВА₁Н - искомый.

Из прямоугольного треугольника АВС находим ВН =$2\sqrt2$.

Из прямоугольного треугольника А₁АВ находим А₁В = 5.

Из прямоугольного треугольника А₁НВ находим sinА₁ = $\frac{BH}{A_{1}B}$ = $\frac{2\sqrt2}{5}$

Ответ: $arcsin\frac{2\sqrt2}{5}$