Дан четырехугольник ABCD такой, что \(\overrightarrow{AD}\) = \(\overrightarrow{AC}\) - \(\overrightarrow{AB}\).
Доказать, что ABCD - параллелограмм.

По формуле (2) имеем

\(\overrightarrow{AC}\) - \(\overrightarrow{AB}\) = \(\overrightarrow{BC}\).

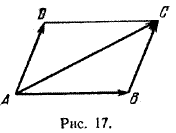
Следовательно, \(\overrightarrow{BC}\) = \(\overrightarrow{AD}\), и поэтому |\(\overrightarrow{BC}\)| = |\(\overrightarrow{AD}\)| и (BC) || (AD). Отсюда следует, что ABCD - параллелограмм (рис. 17).