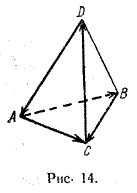
Дана треугольная пирамида ABCD. Найти сумму $\overrightarrow{AB}$ + $\overrightarrow{CD}$ + $\overrightarrow{AC}$

Дана треугольная пирамида ABCD.
Найти сумму $\overrightarrow{AB}$ + $\overrightarrow{CD}$ + $\overrightarrow{AC}$ + $\overrightarrow{BC}$ + $\overrightarrow{DA}$ .

Применив коммутативное и ассоциативное свойства сложения векторов, получим

$\overrightarrow{AB}$ + $\overrightarrow{CD}$ + $\overrightarrow{AC}$ + $\overrightarrow{BC}$ + $\overrightarrow{DA}$ = $\overrightarrow{AB}$ + $\overrightarrow{BC}$ + $\overrightarrow{CD}$ + $\overrightarrow{DA}$ + $\overrightarrow{AC}$ = $\overrightarrow{AC}$ .

« предыдущий

Похожие примеры:

Дана треугольная пирамида ABCD. Найти сумму →AB\overrightarrow{AB} + →CD\overrightarrow{CD} + →AC\overrightarrow{AC} + →BC\overrightarrow{BC} + →DA\overrightarrow{DA}.

Дана треугольная пирамида ABCD.
Найти сумму $\overrightarrow{AB}$ + $\overrightarrow{CD}$ + $\overrightarrow{AC}$ + $\overrightarrow{BC}$ + $\overrightarrow{DA}$ .