Найти сумму \(\overrightarrow{KD}\) + \(\overrightarrow{MC}\) + \(\overrightarrow{DM}\) + \(\overrightarrow{CK}\)

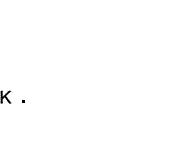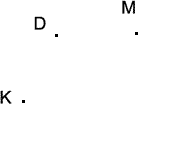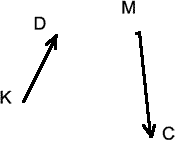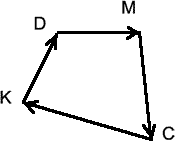
Применяя свойство коммутативности сложения векторов, получаем

\(\overrightarrow{KD}\) + \(\overrightarrow{MC}\) + \(\overrightarrow{DM}\) + \(\overrightarrow{CK}\) = \(\overrightarrow{KD}\) + \(\overrightarrow{DM}\) + \(\overrightarrow{MC}\) + \(\overrightarrow{CK}\).

Теперь по правилу многоугольника находим

\(\overrightarrow{KD}\) + \(\overrightarrow{DM}\)+ \(\overrightarrow{MC}\) + \(\overrightarrow{CK}\) = \(\overrightarrow{KK}\) = 0.