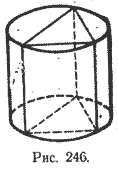
Так как цилиндр и призма имеют одинаковую высоту, то отношение их объемов равно отношению площадей оснований:

$$ \frac{V_ц}{V_п} = \frac{Q_ц}{Q_п} $$

Очевидно, что Q_ц = π R², где R - радиус основания цилиндра.

В основании призмы лежит правильный треугольник, вписанный в окружность радиуса R. Длина его стороны равна √3R и поэтому Q_п = ^3√3/₄ R².

Следовательно,

$$ \frac{V_ц}{V_п} = \frac{4\pi}{3\sqrt3} \approx 2,4 $$