Вычислить площадь трапеции, параллельные стороны которой содержат 16 см и 44 см, а непараллельные 17 см и 25 см.

По условию AD = 44 см и ВС = 16 см.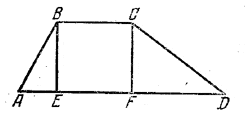

Следовательно, AE+FD = 28 см. Обозначив длину АЕ (в сантиметрах) через х, имеем FD = 28 - x. По условию AB=17 см и СD = 25 см.

Значит, BE² =17² - x² и CF²= 25² - (28 - х)². Получаем уравнение

17² - x² = 25² - (28 - х)²

откуда х =8 (см). Следовательно, находим высоту h:

h = BE = √17²- x² =15 (см).

Теперь находим .

Отв. S = 450 см².