Из вершины S правильной четырехугольной пирамиды на основание опущен перпендикуляр SB. Из середины О отрезка SB опущены перпендикуляр ОМ длиной h на боковое ребро и перпендикуляр ОK длиной b на боковую грань. Найти объем пирамиды.
Пусть Н - высота пирамиды, а - длина стороны основания.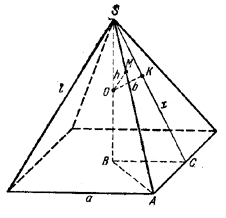
Рассматривая подобные треугольники OMS и ABS, найдем:
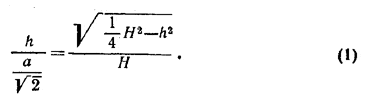
Аналогично из треугольников OKS и CBS получим:
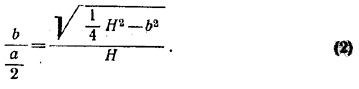
Разделив почленно равенство (1) на (2), будем иметь:

откуда
![]()
Подставив это выражение в (1), легко найдем:
![]()
В итоге для объема V получаем выражение
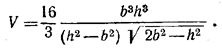
Похожие примеры: