Две окружности касаются друг друга внутренним образом в точке А. Отрезок AB является диаметром большей окружности. Хорда BK большей окружности касается меньшей окружности в точке С. Доказать, что АС является биссектрисой треугольника ABK.

Пусть О — центр меньшей окружности.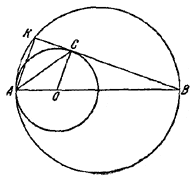

Тогда АК || ОС, так как АК ⊥ BK и ОС ⊥ ВК. Кроме того, ОА = ОС. Следовательно.

∠КАС = ∠АСО = ∠САО.