Три равных окружности пересекаются в одной точке. Вторая точка пересечения каких-либо двух из этих окружностей и центр третьей определяют проходящую через них прямую. Доказать, что получаемые три прямые пересекаются в одной точке.

Докажем, что каждые два из трех отрезков О₁А₁, О₂А₂ и О₃А₃ в точке их пересечения делятся пополам. Отсюда следует, что все три указанные отрезка пересекаются в одной точке.

Например, докажем, что отрезки О₁А₁ и О₂А₂ в точке их пересечения В делятся пополам.

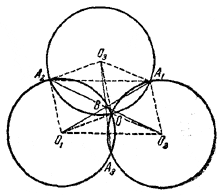
В силу равенства окружностей заключаем, что О₂А₁О₃O — ромб и О₁А₂О₃O — ромб. Отсюда вытекает, что отрезки О₂А₁, ОО₃ и О₁А₂ параллельны и равны.

Поэтому О₁А₂А₁О₂ — параллелограмм и его диагонали O₁A₁ и О₂А₂ в точке пересечения В делятся пополам.