Доказать, что квадрат биссектрисы, проведенной через вершину произвольного треугольника, равен произведению боковых сторон без произведения отрезков основания. Выяснить смысл указанного равенства в случае равнобедренного треугольника.

Пусть z - длина биссектрисы, m, n - длины отрезков, на которые она делит основание треугольника.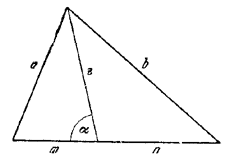

По теореме косинусов

a² = z² + m² — 2mz cos α,

b² = z² + n² + 2nz cosα.

Умножив первое из этих равенств на n , второе на m и сложив, получим:

na² + mb² = (m + n)(z² + mn). (1)

В силу соотношения ^a/_m = ^b/_n имеем:

Подставив это выражение в (1), получим требуемое равенство

ab = z² +mn.

В случае а = b, m = n доказанное равенство выражает теорему Пифагора: а² = z² + m² .