Формула угла между векторами

Угол между двумя векторами

Рассмотрим понятие угла между двумя направлениями в пространстве.

Как и на плоскости, в пространстве направлением называется множество всех лучей, каждый из которых сонаправлен с данным. Таким образом, любой луч из данного множества сонаправленных лучей вполне определяет это направление (подобно тому, как любой направленный отрезок вполне определяет вектор, который он изображает). Поэтому направление в пространстве обычно задают при помощи только одного луча.

Углом между двумя направлениями называется величина наименьшего угла между любыми лучами этих направлений с общим началом.

Угол между лучами l₁ и l₂ обозначается \(\widehat{l_1; l_2}\). По определению угол между двумя направлениями находится в промежутке [0°; 180°].

Углом между двумя ненулевыми векторами называется угол между направлениями этих векторов. Угол между векторами а и b (рис. 21) обозначается \(\widehat{a; b}\)

Если угол между векторами а и b равен 90°, то эти векторы называют перпендикулярными (или ортогональными) и пишут: а ⊥ b.

Отметим, что если а\(\upuparrows\)b, то \(\widehat{a; b}\) = 0°, а если а\(\uparrow\downarrow\)b, то \(\widehat{a; b}\) =180°.

Рассмотрим некоторую прямую l, на которой выбрана единица измерения длины. Пусть А и В - некоторые точки прямой l такие, что |АВ| = 1.

Тогда векторы \(\overrightarrow{AB}\) и \(\overrightarrow{BA}\) называются единичными векторами прямой l (рис.22).

Единичные векторы прямой задают на ней два направления. Одно из них называется положительным, другое - отрицательным.

Прямая, на которой выбрана точка О (начало отсчета), задано положительное направление и задана единица измерения длины, называется осью. Вектор е (|е| = 1), задающий направление оси, называется единичным вектором оси (рис. 23).

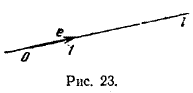
Углом между вектором и осью, называется величина угла между направлением оси и направлением вектора (рис. 24).

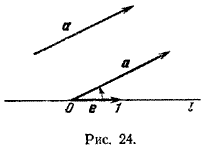
Вычисление угла между двумя векторами.

По определению скалярного произведения

а • b = | а | • | b | cos\(\widehat{(a; b)}\).

Следовательно, если а =/= 0 и b =/= 0, то

$$ cos\widehat{(a; b)} = \frac{a \cdot b}{|a|\cdot|b|} \;\; (1) $$

т. е. косинус угла между ненулевыми векторами а и b равен скалярному произведению этих векторов, деленному на произведение их длин.

Пусть в пространстве имеется прямоугольная декартова система координат, и пусть заданы векторы а = (x₁ ; y₁ ; z₁) и b = (x₂ ; y₂; z₂). Тогда, как известно,

$$ a\cdot b = x_1 x_2 + y_1 y_2 + z_1 z_2, \\ |a|=\sqrt{{x_1}^2 + {y_1}^2 + {z_1}^2}, |b|=\sqrt{{x_2}^2 + {y_2}^2 + {z_2}^2} $$

и поэтому, используя равенство (1), получим формулу

$$ cos\widehat{(a; b)} = \frac{ x_1 x_2 + y_1 y_2 + z_1 z_2}{\sqrt{{x_1}^2 + {y_1}^2 + {z_1}^2}\cdot\sqrt{{x_2}^2 + {y_2}^2 + {z_2}^2} } \;\; (2)$$

Эта формула позволяет вычислить косинус угла между векторами а и b по координатам этих векторов.

Если векторы а = (x₁ ; y₁ ) и b = (x₂ ; y₂) заданы в прямоугольной декартовой системе координат на плоскости, то косинус угла между ними вычисляется по формуле

$$ cos\widehat{(a; b)} = \frac{ x_1 x_2 + y_1 y_2}{\sqrt{{x_1}^2 + {y_1}^2}\cdot\sqrt{{x_2}^2 + {y_2}^2}} \;\; (3)$$

Задача 1. Даны два вектора а = (3; 4) и b = (4; 3). Найти угол между ними.

Подставив координаты векторов в формулу (3), получим

$$ cos\widehat{(a; b)} = \frac{3\cdot 4 + 4\cdot 3}{\sqrt{{3}^2 + {4}^2}\cdot\sqrt{{4}^2 + {3}^2}} = \frac{24}{25} $$

откуда (по таблице) \(\widehat{(a; b)}\) ≈ 16°.

Задача 2. Найти косинус угла между векторами

а = 2i + 2j - k, b = i - 2j + 2k .

Используя формулу (2), получим

$$ cos\widehat{(a; b)} = \frac{ 2\cdot 1 + 2\cdot(-2) + (-1)\cdot 2}{\sqrt{{2}^2 + {2}^2 + {-1}^2}\cdot\sqrt{{1}^2 + {-2}^2 + {2}^2}} = -\frac{4}{9} $$