Проекция вектора на ось. Два свойства проекции
Пусть на плоскости или в пространстве заданы ось l с единичным вектором е и произвольный вектор а.
Ортогональной проекцией (или просто проекцией) вектора а на ось l называется число, равное произведению длины вектора а на косинус угла между векторами е и а.
Проекция вектора а на ось l обозначается символом прl а или пре а.
Таким образом, по определению
прl а = | a | cos\(\widehat{(e, a)}\).
Отложим вектор а от точки О оси l.
Если угол между векторами е и а острый (рис. 50, а), то проекция вектора а на ось l равна длине отрезка ОА1 и где А1 - проекция точки А на прямую l.
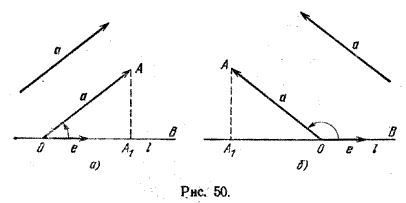
Действительно,
$$ пр_l a = |a|cos\widehat{(e, a)}=|OA|cos\widehat{AOA_1}=|OA_1| $$Если угол между векторами е и а тупой (рис. 50,б), то проекция вектора а на ось l равна длине отрезка ОА1 и взятой со знаком минус.
В самом деле,
$$ пр_l a = |a|cos\widehat{e, a}=|OA|cos\widehat{BOA}= -|OA|cos\widehat{A_{1}OA} = -|OA_1| $$Если вектор а перпендикулярен оси l, то \(\widehat{(e, a)}\) = 90° и прl а = | a | cos 90° = 0.
Рассмотрим два важных свойства проекции вектора на ось.
Свойство 1. Для любых векторов а и b справедливо равенство
прl (а + b) = прl а + прl b, где l - произвольная ось.
Это свойство позволяет заменять проекцию суммы векторов суммой их проекций и наоборот.
Свойство 2. Для любого вектора а и любого числа k справедливо равенство
прl ka = k прl a,
где l - произвольная ось.
Это свойство позволяет выносить и вносить числовой множитель за знак проекции.
Справедливость этих свойств следует из правил действий над векторами, заданными своими координатами.
В самом деле, пусть l - произвольная ось с началом отсчета О и единичным вектором е. Введем прямоугольную систему координат следующим образом (рис. 51).
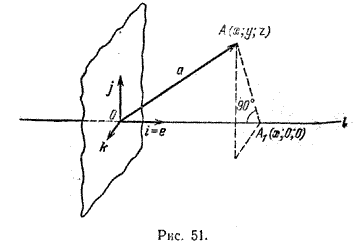
Примем точку О за начало координат, а вектор е - за первый базисный вектор (i = e). В качестве других базисных векторов j и k возьмем любые два единичных перпендикулярных друг другу вектора, лежащих в плоскости перпендикулярной оси l.
Пусть вектор а = \(\overrightarrow{OA}\) имеет координаты х, у, z. Тогда, по определению проекции,
прl а = | a | cos\(\widehat{(i, a)}\).
Но | a | cos\(\widehat{(i, a)}\) = x, т. е. проекция любого вектора на ось l равна абсциссе этого вектора в выбранном нами базисе.
Так как абсцисса суммы векторов равна сумме абсцисс слагаемых векторов, то, следовательно, и проекция суммы векторов на ось l равна сумме проекций этих векторов на ось l.
Точно так же и проекция произведения вектора на число равна произведению этого числа на проекцию вектора, так как при умножении вектора на число его абсцисса умножается на это число.