Сложение и вычитание векторов

Сумма векторов

Пусть даны два вектора а = \(\overrightarrow{OA}\) и b = \(\overrightarrow{OB}\) (рис. 5).

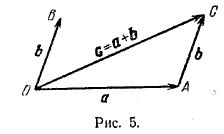
От точки А отложим отрезок АС такой, что \(\overrightarrow{AC}\) = b. Тогда, вектор с = \(\overrightarrow{OC}\) называется суммой векторов а и b и
обозначается а + b.

Таким образом, \(\overrightarrow{OA}\) + \(\overrightarrow{AC}\) = \(\overrightarrow{OC}\). Это равенство называют
правилом треугольника сложения двух векторов.

Oчевидно, что это правило справедливо и в том случае, когда точки О, А и В лежат на одной прямой (рис. 6, 7). В частности, а + 0 = а.

Сложение векторов обладает следующими свойствами:

1. Свойство коммутативности (перестановочности): для любых векторов а и b

а + b = b + а. (1)

2. Свойство ассоциативности (сочетательности): для любых векторов а, b и с

(а + b) + с = а + (b + с). (2)

1. Пусть a = \(\overrightarrow{OA}\), b = \(\overrightarrow{OB}\). Рассмотрим случай, когда точки О, А и В не лежат на одной прямой. На отрезках ОА и ОВ построим параллелограмм OACB (рис. 8).

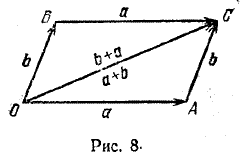
Тогда |ОА| = |ВС|, (ОА) || (ВС) и |ОВ| = |АС|, (ОВ) || (АС), как противоположные стороны параллелограмма. Следовательно,

а = \(\overrightarrow{OA}\)= \(\overrightarrow{BC}\), b = \(\overrightarrow{OB}\) = \(\overrightarrow{AC}\),

и поэтому

а + b = \(\overrightarrow{OA}\)+ \(\overrightarrow{AC}\) = \(\overrightarrow{OC}\),
b + а = \(\overrightarrow{OB}\) + \(\overrightarrow{BC}\) = \(\overrightarrow{OC}\),

что и доказывает равенство (1).

Для случая, когда точки О, А, В лежат на одной прямой, доказательство можно провести самостоятельно.

2. От некоторой точки О отложим вектор \(\overrightarrow{OA}\) = а, от точки А отложим вектор \(\overrightarrow{AB}\) = b и, наконец, от точки В отложим вектор \(\overrightarrow{BC}\) = с (рис. 9, 10).

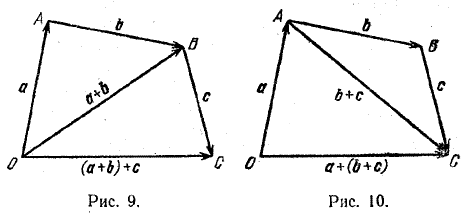
Соединим точки О и С отрезком ОС. Тогда, с одной стороны (см. рис. 9),

(а + b) + с = (\(\overrightarrow{OA}\) + \(\overrightarrow{AB}\)) + \(\overrightarrow{BC}\) =
\(\overrightarrow{OB}\) + \(\overrightarrow{BC}\)= \(\overrightarrow{OC}\)

и, с другой стороны (см. рис. 10),

а + (b + с) = \(\overrightarrow{OA}\) + (\(\overrightarrow{AB}\)+ \(\overrightarrow{BC}\)) = \(\overrightarrow{OA}\) + \(\overrightarrow{AC}\) = \(\overrightarrow{OC}\),

что и доказывает равенство (2).

Из риc. 8 видно, что сумма векторов а = \(\overrightarrow{OA}\) и b = \(\overrightarrow{OB}\) равна направленной диагонали \(\overrightarrow{OC}\) параллелограмма OACB, построенного на отрезках ОА и ОВ, т.е.

\(\overrightarrow{OA}\) + \(\overrightarrow{OB}\) = \(\overrightarrow{OC}\).

Это равенство называется правилом параллелограмма сложения двух векторов.

Так как сложение векторов ассоциативно, то сумма трех и большего числа векторов записывается без скобок. Например, вместо (а + b) + с или а + ( b + с ) пишут а + b + с.

Если требуется найти сумму трех или большего числа векторов, то применяют так называемое правило многоугольника. Оно состоит в следующем.

Пусть даны векторы а, b, с, d и требуется найти их сумму.

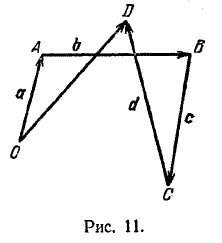
Выберем некоторую точку О (рис. 11) и построим отрезок ОА такой, что \(\overrightarrow{OA}\) = а,
затем построим отрезок АВ такой, что \(\overrightarrow{AB}\) = b, и т. д.

Построение продолжается до тех пор, пока не будут исчерпаны все векторы-слагаемые. Направленный отрезок \(\overrightarrow{OD}\), замыкающий полученную ломаную, будет равен сумме данных векторов.

Противоположные векторы. Вычитание векторов.

Любые два вектора, сумма которых равна нулевому вектору, называются противоположными. Вектор, протипоположный вектору а, обозначается - а. Следовательно, по определению

а + (- а) = 0.

Из определения следует, что если а = \(\overrightarrow{AB}\), то - а = \(\overrightarrow{BA}\), т. е. противоположные векторы имеют одинаковую длину и противоположные направления.

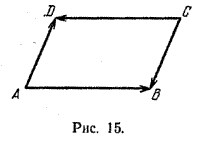
Например, если ABCD - параллелограмм, то векторы \(\overrightarrow{AB}\) и \(\overrightarrow{CD}\) противоположные (рис. 15). Векторы \(\overrightarrow{AD}\) и \(\overrightarrow{CB}\) тоже противоположные.

Для любых двух векторов а и b вектор с = а + (- b) называется разностью векторов а и b и обозначается а - b. Таким образом, по определению

а - b = а + (- b).

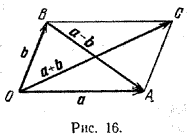
Если а = \(\overrightarrow{OA}\) и b = \(\overrightarrow{OB}\) (рис. 16), то

а - b = \(\overrightarrow{OA}\) - \(\overrightarrow{OB}\) = \(\overrightarrow{OA}\) + \(\overrightarrow{BO}\) = \(\overrightarrow{BO}\)+ \(\overrightarrow{OA}\) = \(\overrightarrow{BA}\).

Следовательно,

\(\overrightarrow{OA}\) - \(\overrightarrow{OB}\) = \(\overrightarrow{BA}\) (1)

Из рисунка видно, что \(\overrightarrow{BA}\) - это направленная диагональ параллелограмма ОАСВ, построенного на отрезках ОА и ОВ. Другая диагональ \(\overrightarrow{OC}\) изображает сумму векторов \(\overrightarrow{OA}\) и \(\overrightarrow{OB}\).

Нетрудно заметить, что формулу (1) можно применять, не прибегая к чертежу: для этого достаточно внимательно проследить за порядком расположения букв в записи данных и искомого векторов. Так, например,

$$ \overrightarrow{PQ} - \overrightarrow{PN} = \overrightarrow{NQ}\;\; (2)$$