Компланарные вектора
Из курса геометрии известно, что прямая параллельна плоскости, если она не имеет с этой плоскостью общих точек или лежит на ней.
Вектор \(\overrightarrow{AB}\) назовем параллельным плоскости, если прямая АВ параллельна этой плоскости. Нулевой вектор считается параллельным любой плоскости.
Векторы a1, a2, ..., an называются компланарными, если каждый из них параллелен одной и той же плоскости.
Любые два вектора всегда компланарны.
Очевидно, если три вектора компланарны, то их можно изобразить направленными отрезками, лежащими в одной плоскости.
Рассмотрим сложение трех некомпланарных векторов по так называемому «правилу параллелепипеда».
Пусть векторы а, b и с некомпланарны (рис. 28).
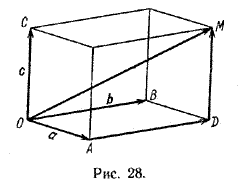
От произвольной точки О отложим векторы \(\overrightarrow{OA}\) = а, \(\overrightarrow{OB}\) = b и \(\overrightarrow{OC}\) = с и построим параллелепипед, для которого [ОА], [ОВ] и [ОС] являются ребрами. Пусть [ОМ]-диагональ этого параллелепипеда. Так как
\(\overrightarrow{OB}\) = \(\overrightarrow{AD}\), \(\overrightarrow{OC}\) = \(\overrightarrow{DM}\),
то
\(\overrightarrow{OA}\) + \(\overrightarrow{OB}\) + \(\overrightarrow{OC}\)
= \(\overrightarrow{OA}\) + \(\overrightarrow{AD}\) + \(\overrightarrow{DM}\) = \(\overrightarrow{OM}\),
т. е. а + b + с = \(\overrightarrow{OM}\).
Итак, сумма трех некомпланарных векторов равна вектору, изображаемому направленной диагональю параллелепипеда, построенного на этих векторах.
Задача. Привести примеры ребер треугольной пирамиды ABCD изображающих: а) два коллинеарных вектора; б) три компланарных вектора; в) три некомпланарных вектора.
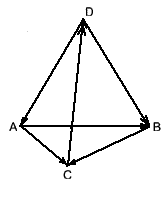
Рассмотрим изображение пирамиды (рис. 29). Используя определения коллинеарных и компланарных векторов, получим:
а) никакие два различных ребра пирамиды не могут изображать коллинеарные векторы, так как среди них нет взаимно параллельных;
б) ребра АС, СВ, ВА (или ребра AD, DC и АС) изображают три компланарных вектора (например, векторы \(\overrightarrow{AC}\), \(\overrightarrow{AB}\) и \(\overrightarrow{BC}\));
в) ребра DA, DC и DB изображают три некомпланарных вектора (например, векторы \(\overrightarrow{DA}\), \(\overrightarrow{CD}\), \(\overrightarrow{DB}\)).