Свойства скалярного произведения векторов

Скалярное произведение двух векторов.

В физике работа А постоянной силы F при прямолинейном движении материальной точки из положения В в положение С (рис. 52) вычисляется по формуле

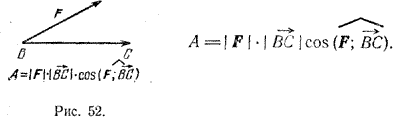
Эта формула вектору силы F и вектору перемещения ВС ставит в соответствие скалярную величину - работу. Величину А называют скалярным произведением векторов F и $\overrightarrow{BC}$. Скалярное произведение может быть определено для любых двух векторов. Оно широко используется в физике и в математике.

Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Если из двух векторов хотя бы один нулевой, то скалярное произведение этих векторов принимается равным нулю.

Скалярное произведение векторов а и b обозначается а • b. Итак, по определению

а • b = | а | • | b | cos$\widehat{(a; b)}$. (1)

Если а = b, то скалярное произведение принимает вид а • a и называется скалярным квадратом вектора а и обозначается символом a². Очевидно, что a² = а • a = |а|².

Как известно, проекция вектора b на ось, направление которой совпадает с направлением вектора а, выражается формулой

пр_ab = | b | cos$\widehat{(a; b)}$. (2)

Используя формулы (1) и (2), можно записать

а • b = | а | np_ab. (3)

Таким образом, скалярное произведение двух векторов равно произведению длины одного из них и проекции второго вектора на направление первого.

Аналогично получается формула а • b = | b | np_ba.

Задача 1. Известно, что | а | = 2, | b | = ¹/₃, $\widehat{(a; b)}$ = 150°. Найти а • b .

По формуле (1) находим

а • b = | а | • | b | cos$\widehat{(a; b)}$ = 2 • ¹/₃ • 150°

Задача 2. Найти всевозможные скалярные произведения базисных векторов i и j прямоугольной декартовой системы координат на плоскости.

По определению скалярного произведения

i • j = | i | • | j | cos 90° = 1 • 1 • 0 = 0,

i² = i • i = | i | • | i | cos 0° = 1 • 1 • 1 = 1.

Аналогично j • i = 0, j² = 1.

Задача 3. Какой знак имеет скалярное произведение векторов а и b, если
90° < $\widehat{(a; b)}$ < 180°?

Так как в формуле а • b = | а | • | b | cos $\widehat{(a; b)}$ числа | а | и | b | неотрицательны, знак а • b зависит от знака косинуса.

В промежутке ] 90°; 180°] cos $\widehat{(a; b)}$ < 0, поэтому а • b < 0.

Задача 4. В каком промежутке находится величина угла между векторами а и b, если а • b > 0?

Так как а • b > 0, то | а | =/= 0, | b | =/= 0 и cos $\widehat{(a; b)}$ > 0. Отсюда $\widehat{(a; b)}$ $\in$ [0°; 90° [.

Свойства скалярного произведения векторов

1. Скалярное умножение векторов обладает переместительным свойством:

а Х b = b Х а. (1)

Так как

$\widehat{(a; b)}$ = $\widehat{(b; a)}$ и | а | Х | b | = | b | Х | а |,

то

а Х b = | а | Х | b | cos $\widehat{(a; b)}$ = | b | Х | а | cos$\widehat{(b; a)}$ = b Х а.

Если а = 0 или b = 0, то по определению скалярного произведения а Х b = 0 и b Х а = 0, т. е. а Х b = b Х а

2. Скалярное умножение векторов обладает сочетательным свойством по отношению к умножению вектора на число:

(ka) Х b = k (а Х b). (2)

Обозначим $\widehat{(a; b)}$ = φ и $\widehat{(ka; b)}$ = φ₁.

Если k > 0, то $\widehat{(a; b)}$ = $\widehat{(ka; b)}$, т. е. φ = φ₁ и тогда

(ka) Х b = | kа | Х | b | cos φ₁ = k | а | Х | b | cos φ = k (а Х b).

Если k < 0, то ka $\uparrow\downarrow$ a и φ₁ = 180° Ч φ, и тогда

(ka) Х b = | kа | Х | b | cos φ₁ = | k | Х | а | Х | b | cos (180° Ч φ) =
= Ч k Х | а | Х | b |(Ч cos φ) =

= k | а | Х | b | cos φ = k (а Х b)

Если k = 0 или a = 0, или b = 0, то

(ka) Х b = 0 и k (а Х b) = 0, и поэтому (ka) Х b =k (а Х b).

3. Скалярное умножение векторов обладает распределительным свойством относительно сложения векторов

а Х (b + с) = а Х b + а Х c. (3)

Если a = 0, то свойство (3) очевидно.

Пусть a =/= 0. Тогда

а Х (b + с) = | a | Х np_a(b + c) = | a | Х (np_ab + np_ac) =
= | a | Х np_ab + | a | Х np_ac = а Х b + а Х c.

В ходе доказательства были использованы известные свойства проекции вектора на ось.

Заметим, что из (1) и (3) следует формула

(a + b) Х c = a Х c + b Х c. (4)

Сходство свойств скалярного произведения векторов со свойствами произведения действительных чисел позволяет легко производить вычисления и преобразования со скалярными произведениями.

Задача. Доказать тождество

(a + b) ² = а² + 2a Х b + b².

Используя свойства (1) и (4) скалярного произведения, получаем

(a + b) ² = (a + b) Х (a + b) = (a + b) Х а + (a + b) Х b =
= aХa + bХa + aХb + bХb = а² + aХb + aХb + b² =

= а² + 2a Х b + b²

Теорема. Для того чтобы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю:

(а =/= 0, b =/= 0, a Х b = 0 ) <==> a ⊥ b. (5)

Необходимость. Пусть a ⊥ b. Тогда

φ = $\widehat{(a; b)}$ = 90° и a Х b = | а | Х | b | Х cos 90° = 0.

Достаточность. Пусть a Х b = 0 , а =/= 0, b =/= 0.

Так как а =/= 0, b =/= 0, то | а | =/= 0, | b | =/= 0, а так как | а | Х | b | Х cos φ = 0, то cos φ = 0 и, следовательно, φ = 90°, т. е. a ⊥ b.