Разложение вектора по трем некомпланарным векторам

Теорема. Любой вектор m может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых некомпланарных векторов а, b и с:

m = xa + yb + zc. (1)

Прежде всего отметим, что никакие два вектора из векторов а, b, с не коллинеарны; в противном случае векторы а, b, с были бы компланарны. Поэтому, если вектор m компланарен с какими-нибудь двумя векторами (например, с а и b), то m = ха + уb и, следовательно,

m = ха + уb + 0 • с,

т. е. в этом случае теорема доказана.

Пусть вектор m не компланарен ни с какими двумя векторами из векторов а, b, с (рис. 30).

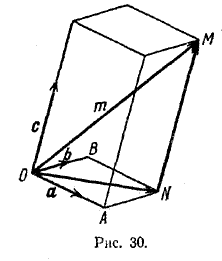
Приведем все векторы к общему началу О и проведем через точку М (конец направленного отрезка, изображающего вектор \(\overrightarrow{OM}\) = т) прямую, параллельную вектору с. Эта прямая пересечет плоскость ОАВ в некоторой точке N. Ясно, что

\(\overrightarrow{OM}\) = \(\overrightarrow{ON}\) + \(\overrightarrow{NM}\).

По свойству коллинеарных векторов \(\overrightarrow{NM}\) = zc.

По теореме о разложении вектора по двум неколлинеарным векторам существуют числа х, у такие, что \(\overrightarrow{ON}\) = ха + уb.

Таким образом,

\(\overrightarrow{OM}\) = \(\overrightarrow{ON}\) + \(\overrightarrow{NM}\) = xa + yb + zc.

Единственность разложения вектора т по векторам а, b и с: доказывается аналогично тому, как это было сделано в теореме о разложении вектора по двум неколлинеарным векторам.

Базисом пространства называются любые три некомпланарных вектора, взятые в определенном порядке.

Пусть e₁, e₂ и e₃ - некоторый базис, и a - произвольный вектор. Тогда, по только что доказанной теореме, существуют три числа х, у, z таких, что

а = хe₁ + уe₂ + ze₃.

Числа х, у и z называются координатами вектора а в данном базисе. В этом случае пишут а = (х; у; z).

Задача 1. Дан куб ABCDA₁B₁C₁D₁. Разложить вектор \(\overrightarrow{AK}\), где K - центр грани ВСС₁В₁ по векторам а = \(\overrightarrow{AB}\), b = \(\overrightarrow{AC}\), с = \(\overrightarrow{AA}\) (рис. 31).

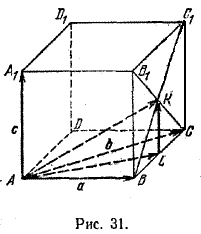
Из \(\Delta\)AKL имеем \(\overrightarrow{AK}\) = \(\overrightarrow{AL}\) + \(\overrightarrow{LK}\), но

$$ \overrightarrow{AL} = \frac{\overrightarrow{AB}+\overrightarrow{AC}}{2} = \frac{a+b}{2} $$
$$ а \;\; \overrightarrow{LK} = \frac{\overrightarrow{AA_1}}{2} = \frac{c}{2} $$

Следовательно,

$$ \overrightarrow{AK} = \frac{a+b}{2} + \frac{c}{2} = \frac{1}{2}a + \frac{1}{2}b + \frac{1}{2}c $$

Задача 2. Пусть векторы \(\overrightarrow{DA}\), \(\overrightarrow{DB}\), \(\overrightarrow{DC}\), изображенные соответствующими направленными ребрами треугольной пирамиды ABCD, образуют базис. Найти координаты вектора \(\overrightarrow{AB}\) в этом базисе.

Воспользуемся рис. 29a.

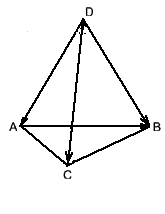
Обозначив \(\overrightarrow{DA}\) = e₁, \(\overrightarrow{DB}\) = e₂, \(\overrightarrow{DC}\) = e₃, получим \(\overrightarrow{AB}\) = \(\overrightarrow{DB}\) - \(\overrightarrow{DA}\) = - e₁ + e₂ или \(\overrightarrow{AB}\) = - 1•e₁ + 1•e₂ + 0•e₃,

откуда \(\overrightarrow{AB}\) = (- 1; 1; 0).