Коллинеарные вектора

Два ненулевых вектора, направления которых совпадают или противоположны, называются коллинеарными.

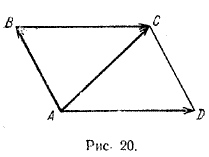
Так, например, на рис. 20 векторы \(\overrightarrow{BC}\) и \(\overrightarrow{AD}\) коллинеарны, а векторы \(\overrightarrow{AB}\) и \(\overrightarrow{AC}\) неколлинеарны.

Если векторы а и b коллинеарны, то говорят также, что вектор а коллинеарен вектору b, а вектор b коллинеарен вектору а.

Нулевой вектор считается коллинеарным любому вектору.

Теорема (признак коллинеарности). Для того чтобы вектор а был коллинеарен ненулевому вектору b, необходимо и достаточно, чтобы существовало число k, удовлетворяющее условию

a = kb. (1)

Достаточность. Если при некотором k равенство (1) выполняется, то векторы b и а коллинеарны по определению умножения вектора на число и определению коллинеарных векторов.

Необходимость. Пусть вектор а коллинеарен ненулевому вектору b. Возможны следующие три случая: а \(\upuparrows\) b, а \(\uparrow\downarrow\) b, а = 0.

Если а \(\upuparrows\) b, то a = \(\frac{|a|}{|b|}\) • b, т. е. равенство (1) выполняется при k = \(\frac{|a|}{|b|}\)

Если а \(\uparrow\downarrow\) b , то a = - \(\frac{|a|}{|b|}\) • b, т. е. равенство (1) выполняется при k = - \(\frac{|a|}{|b|}\)

Если а = 0, то а = 0 • b , т. е. равенство (1) выполняется при k= 0.

Задача. Доказать, что векторы \(\overrightarrow{AB}\) + \(\overrightarrow{CB}\) + 2\(\overrightarrow{BA}\) и ¹/₃ \(\overrightarrow{AC}\) коллинеарны.

Используя свойства операций над векторами, получим

\(\overrightarrow{AB}\) + \(\overrightarrow{CB}\) + 2\(\overrightarrow{BA}\) = (\(\overrightarrow{AB}\) + \(\overrightarrow{BA}\)) + (\(\overrightarrow{CB}\) + \(\overrightarrow{BA}\)) = 0 + \(\overrightarrow{BA}\) = \(\overrightarrow{BA}\) = - \(\overrightarrow{AC}\).

Таким образом,

\(\overrightarrow{AB}\) + \(\overrightarrow{CB}\) + 2\(\overrightarrow{BA}\) = -3 (¹/₃ \(\overrightarrow{AC}\)) .

По признаку коллинеарности векторов данные в условии векторы коллинеарны.