Векторы. Основные понятия

Любой отрезок прямой имеет две концевые точки. Если одна из них принята за начало отрезка, а другая - за конец, то такой отрезок называется направленным. Направленные отрезки обычно обозначаются двумя буквами со стрелкой, например, \(\overrightarrow{AB}\), \(\overrightarrow{BA}\), \(\overrightarrow{OA}\), \(\overrightarrow{OB}\) и т. д., где первая буква обозначает начало отрезка, а вторая буква - конец отрезка.

Два направленных отрезка считаются равными, если они имеют равные длины, параллельны и направлены в одну сторону.

Например, на рис. 4, где ABCD - параллелограмм, направленные отрезки \(\overrightarrow{AB}\) и \(\overrightarrow{DC}\) равны, так как |АВ| = |DC|, (AB) || (DC) и отрезки \(\overrightarrow{AB}\) и \(\overrightarrow{DC}\) направлены в одну сторону.

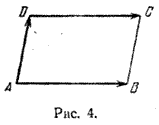
Направленные отрезки \(\overrightarrow{AB}\) и \(\overrightarrow{AD}\) не являются равными, так как они не параллельны. Направленные отрезки \(\overrightarrow{AB}\) и \(\overrightarrow{CD}\) тоже не являются равными, так как они имеют противоположные направления, хотя они параллельны и имеют равные длины.

Направленные отрезки с введенным понятием равенства называются векторами. В следующих параграфах дли них будут введены операции сложения, вычитания и умножения на число.

Согласно определению все равные между собой направленные отрезки изображают один и тот же вектор. Например, если вектор, изображенный на рис. 4 направленным отрезком \(\overrightarrow{AB}\), обозначить а, то а = \(\overrightarrow{AB}\) = \(\overrightarrow{CD}\).

Длина вектора а = \(\overrightarrow{AB}\), обозначаемая | а | или | \(\overrightarrow{AB}\)| - это длина отрезка АВ.

Направление вектора а = \(\overrightarrow{AB}\) - это направление, определяемое лучом АВ.

Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 0. Очевидно, что у нулевого вектора начало совпадает с концом: 0 = \(\overrightarrow{AA}\) = \(\overrightarrow{BB}\).

Таким образом, каждый вектор а =/= 0 вполне определяется длиной и направлением. Нулевой вектор направления не имеет.