Умножение вектора на число

Произведением ненулевого вектора а на число х =/= 0 называется вектор, длина которого равна | x | • | а |, а направление совпадает с направлением а, если х > 0, и противоположно ему, если х < 0.

Произведением нулевого вектора на любое число х и произведением любого вектора на число нуль называется нулевой вектор.

Произведение вектора а на число х обозначается х • а (числовой множитель пишется слева).

Согласно определению | x • а | = | x | • | а | для любого вектора а и любого числа х.

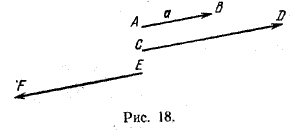
На рис. 18 изображены произведения вектора а на число х = 2 (вектор \(\overrightarrow{CD}\)) и на число х = -2 (вектор \(\overrightarrow{EF}\)).

Умножение вектора на число обладает следующими свойствами:

1. Свойство ассоциативности (сочетательности):

х • (у • а) = (х • у) • а.

2. Свойство дистрибутивности (распределительности) относительно векторного множителя:

х • а + y • а = (х + у) • а.

3. Свойство дистрибутивности (распределительности) относительно числового множителя:

х • а + х • b = х • (a + b).

Если a = 0 или xy = 0, то равенство х(уа) = = (xy)а очевидно, так как слева и справа стоят нулевые векторы.

Пусть а =/= 0, xy =/= 0 и а = \(\overrightarrow{OA}\). Тогда векторы х (у • \(\overrightarrow{OA}\)) и (xy) \(\overrightarrow{OA}\) лежат на прямой \(\overrightarrow{OA}\), имеют длину |x| • |y| • |\(\overrightarrow{OA}\)| и направлены в одну сторону: в сторону вектора а = \(\overrightarrow{OA}\), если xy > 0, и в противоположную сторону, если xy < 0. Таким образом, свойство 1 доказано.

Свойства 2 и 3 доказывать не будем. Заметим лишь, что свойства 1 и 2 являются свойствами векторов на прямой. Свойство 3 является свойством векторов на плоскости; оно тоже было доказано.

Задача. В параллелограмме ABCD точка М есть точка пересечения диагоналей. Найти множитель k в каждом из следующих случаев:

1) \(\overrightarrow{M C}\) = k • \(\overrightarrow{CA}\); 2) \(\overrightarrow{BD}\) = k • \(\overrightarrow{BM}\); 3) \(\overrightarrow{AC}\) = k • \(\overrightarrow{CM}\);

4) \(\overrightarrow{BB}\) = k • \(\overrightarrow{BD}\); 5) \(\overrightarrow{AA}\) = k • \(\overrightarrow{CC}\).

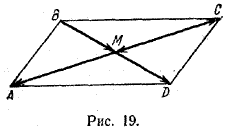
В соответствии с определением умножения вектора на число имеем (рис. 19)

1) \(\overrightarrow{M C} \uparrow\downarrow \overrightarrow{CA}\), | CA| = 2•| MC |, откуда k = - ¹/₂;

2) \(\overrightarrow{BM}\upuparrows\overrightarrow{BD}\), | BD | = 2 • | ВМ |, откуда k = 2;

3) \(\overrightarrow{CM}\uparrow\downarrow \overrightarrow{AC}\), | CM | = ¹/₂• |AС |, откуда k = -2;

4) \(\overrightarrow{BB}\) = 0, \(\overrightarrow{BD}\) =/= 0, откуда k = 0;

5) \(\overrightarrow{AA}\) = 0, \(\overrightarrow{CC}\) = 0, откуда k - любое число.