Дан параллелепипед ABCDA₁B₁C₁D₁.
Найти сумму векторов \( \overrightarrow{AB}, \overrightarrow{B_{1}C_{1}}, \overrightarrow{CC_{1}}, \overrightarrow{B_{1}A_{1}}, \overrightarrow{B_{1}B} \)

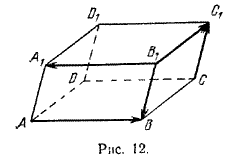
Из свойств ребер параллелепипеда следует, что

$$ \overrightarrow{B_{1}C_{1}}=\overrightarrow{BC}, \overrightarrow{B_{1}A_{1}}=\overrightarrow{C_{1}D_{1}}, \overrightarrow{B_{1}B}=\overrightarrow{D_{1}D} $$

Поэтому

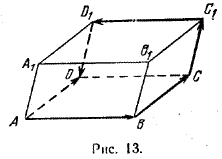
$$ \overrightarrow{AB}+\overrightarrow{B_{1}C_{1}}+\overrightarrow{CC_{1}}+\overrightarrow{B_{1}A_{1}}+\overrightarrow{B_{1}B}=\\= \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC_{1}}+\overrightarrow{C_{1}D_{1}}+\overrightarrow{D_{1}D} $$

Применив правило многоугольника, получим (рис. 13)

$$ \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC_{1}}+\overrightarrow{C_{1}D_{1}}+\overrightarrow{D_{1}D}=\overrightarrow{AD} $$