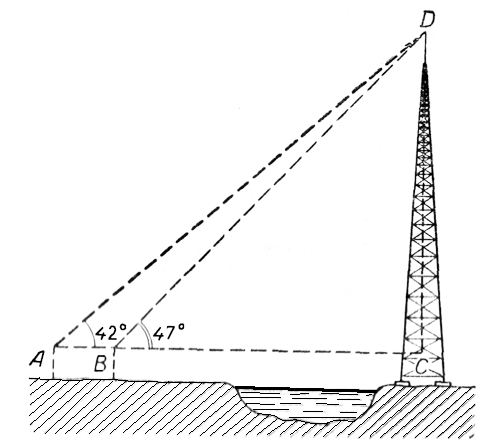
В тpeyгольнике BCD измеряем ∠DBC, пусть он равен 47°.

$$ \frac{CD}{AC}=tg42°; \;\; \frac{CD}{BC}=tg47° $$

\( AC=\frac{CD}{tg42°} \;\; BC=\frac{CD}{tg47°} \) (точки A, B, С находятся на одной прямой)

$$ AC - BC = \frac{CD}{tg42°} - \frac{CD}{tg47°} = CD(\frac{1}{tg42°}-\frac{1}{tg47°}) $$ $$ AC - BC = CD(\frac{1}{0,9004}-\frac{1}{1,0724}) $$

Расстояние АС — ВС, т. е. АВ, может быть непосредственно измерено, пусть оно равно 12,0 м, тогда

12,0 = CD(1,1106 — 0,9325) = CD • 0,1781.

Откуда \( CD = \frac{12}{0,1781} \approx 67,4 м \)

Для окончательного определения высоты антенны к 67,4 м следует прибавить высоту прибора, с помощью которого определяли углы А и В. Если высота прибора, например, составляла 1,40 м, то окончательно высота антенны будет равна 67,4 + 1,40 = 68,8 (м).