В тетраэдр, у которого ребро равно а, вписан шар так, что он касается всех ребер тетраэдра. Определить радиус этого шара и объем части шара, расположенной вне тетраэдра.
Центр шара, касающегося ребер тетраэдра ABCQ (рис.), совпадает с центром тетраэдра (т. е. с точкой О, равноотстоящей от вершим А, В, С, D), а точки касания шара с ребрами суть середины ребер. Например, точка касания N есть середина ребра AD. Действительно, все шесть равнобедренных треугольников АОВ, ВОС, СОА, BOD, COD и AOD (начерчен только треугольник AOD) равны друг другу (по трем сторонам). Следовательно, их высоты ОМ, ON и т. д. равны. Поэтому, если описать шар радиусом ON = r, то он пройдет через середины L, М, N, Q, K, R ребер и там коснется их (так как ON⊥AD и т, д.).
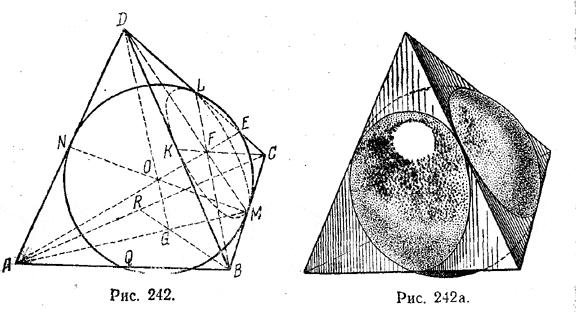
Проведем через высоту тетраэдра DG и ребро AD плоскость ADG. Она будет перпендикулярна к ребру ВС (доказательство дано в задаче 460) и пересечет это ребро в его середине М. В сечении получим равнобедренный треугольник AMD (AM=MD). Проведем высоту MN этого треугольника (N - середина AD). Центр О лежит на MN (так как он равноудален от А и О). Следовательно, MO=NO. Значит, r = MN/2. Высота MN определяется из треугольника ANM, где AN = a/2 и AM = a√3/2. (как апофема равностороннего треугольника ABC). Имеем
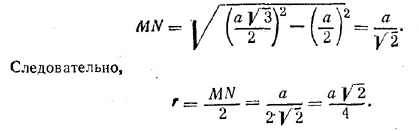
Часть шара, расположенная вне тетраэдра, состоит из четырех равных сегментов, отсекаемых от шара гранями тетраэдрa. Рассмотрим одну из граней BDC. Круг LMK, лежащий в основании сегмента, вписан в равносторонний треугольник BDC (ибо стороны треугольника касаются шара; значит, они касаются и малого кругa LMK, лежащего в плоскости BDC). Радиус этого круга FM = a√3/6
Следовательно,
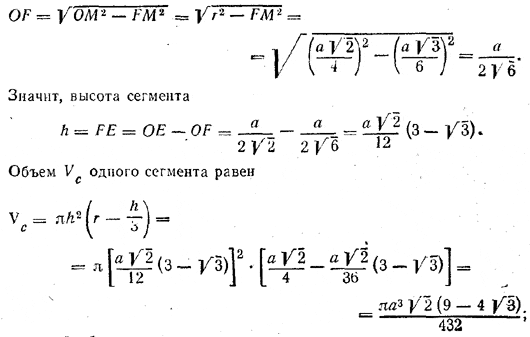
искомый объем
V = 4Vc
Замечание. Круг LKM, вписанный в треугольник BCD. изображается эллипсом, который легко будет начертить от руки, если кроме точек К, L, М предварительно отметить еще три точки, соответственно симметричные с ними относительно F (точка F есть точка пересечения медиан треугольника BDC).
![]()