Полная поверхность правильной четырехугольной пирамиды равна S, а плоский угол боковой грани при вершине равен α. Найти высоту пирамиды.

По условию a2+2a • ME = S (рис.).

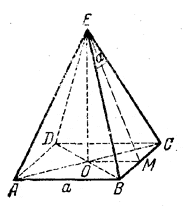
Но из треугольника ВМЕ имеем ME = a/2 ctg α/2 следовательно, S = a2(1 + ctg α/2); отсюда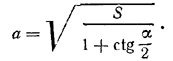

Теперь из треугольника ОМЕ находим

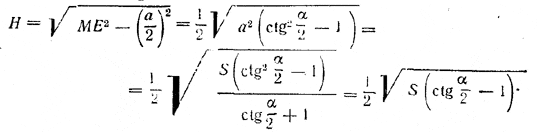
Выражение ctg α/2 - 1 можно преобразовать:





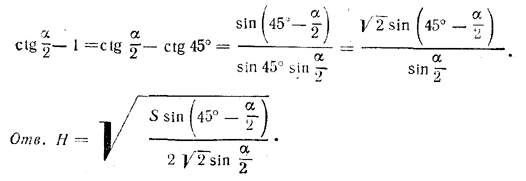
Похожие примеры:
Основанием пирамиды служит квадрат. Две противоположные грани — равнобедренные треугольники, одна из них образует с основанием внутренний угол β, а другая — внешний острый угол α. Высота пирамиды равна Н. Найти объем пирамиды и углы, образованные двумя другими боковыми гранями с плоскостью основания. Смотреть решение→
В основании пирамиды лежит прямоугольник. Одна из боковых граней наклонена к основанию под углом β= 90°— α, а противоположная ей грань перпендикулярна к основанию и имеет вид прямоугольного треугольника с прямым углом при вершине пирамиды и острым углом, равным α. Сумма высот этих двух граней равна m. Определить объем пирамиды и сумму площадей двух других боковых граней. Смотреть решение→
В основании пирамиды лежит прямоугольный треугольник, у которого один острый угол равен αи радиус вписанного круга равен r. Каждая из боковых граней образует с основанием угол α. Определить объем, боковую и полную поверхность пирамиды. Смотреть решение→